
Summer 2022
Pascal’s Triangle is a mathematical triangular array. It is named after French mathematician Blaise Pascal, but it was used in China at least 300 years before Pascal was born.

Pascal’s triangle looks like a triangle with 1 number at the top and then each row having one more number—so, 2 numbers in the second row, 3 numbers in the third row, etc. Actually, for Pascal’s Triangle, we start counting the rows with zero, because each row represents the largest exponent in the expression. Zero is an acceptable exponent for a term, so we start with zero. So, 1 by itself is the number in the “zeroth” row, 1 and 1 are the numbers in the “first” row, etc.
The triangle can be used to find out the coefficients of the terms of a binomial raised to a positive power. For example, (x+1)4 would not be much fun to calculate by hand, but with Pascal’s Triangle, we can just look at the fifth row (because the fifth row would be an expression to the fourth power — remember, we started with zero). In the fifth row, we see “1 4 6 4 1”. So, (x+1)4 will be x4 + 4x3 + 6x2 + 4x + 1.
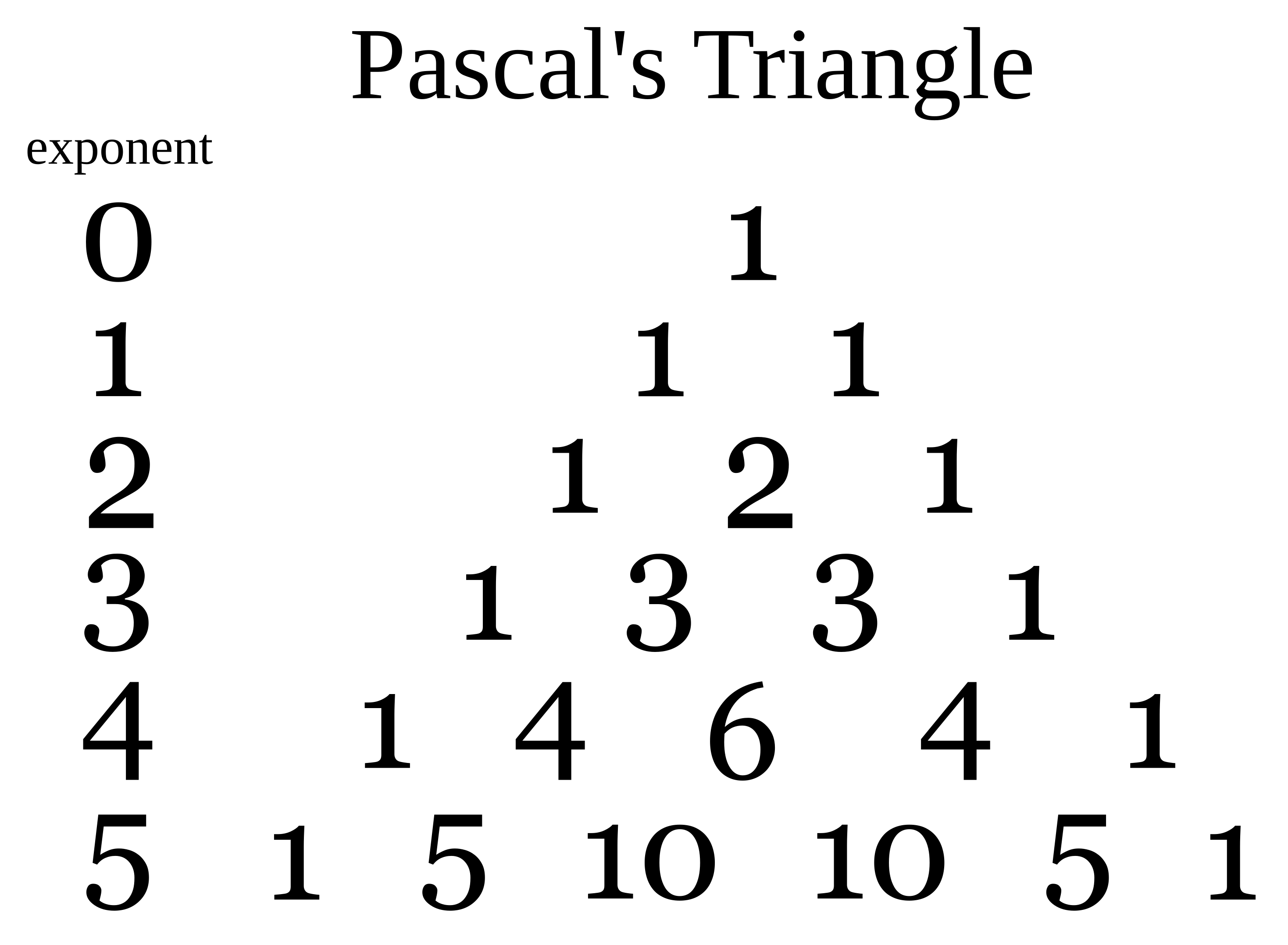
The triangle can be made as follows:
In the first row, write only the number 1.
In the second row, write the number 1 twice.
To get the numbers of following rows, add the two numbers to the left and right in the row above. If there is no number to the left or to the right, then pretend that that number is zero. That is why both numbers in the second row are 1—we pretend that the first row is 010.
Continue like this for as many rows as you need.
Be careful to keep track of the exponents that go with each row (as in the image). People sometimes forget to start with zero, and end up using numbers from the wrong row when they write out the expression. The third row, for example, is for a binomial raised to the second power.
This document includes or is based on content from the following files:
at Simple Wikipedia. Accessed 2022 July 13; published under the Creative Commons Attribution-ShareAlike 3.0 Unported License. https://simple.wikipedia.org/wiki/Binomial_expansion
at Simple Wikipedia. Accessed 2022 July 13; published under the Creative Commons Attribution-ShareAlike 3.0 Unported License. https://simple.wikipedia.org/wiki/Pascal%27s_Triangle
at Wikipedia. Accessed 2022 July 13; published under the Creative Commons Attribution-ShareAlike 3.0 Unported License. https://en.wikipedia.org/wiki/Blaise_Pascal
graphics file from Wikipedia. Accessed 2022 July 13; published under the Creative Commons Attribution-ShareAlike 3.0 Unported License. https://en.wikipedia.org/wiki/File:Pascal%27s_triangle_5.svg
image from Wikipedia. Accessed 2022 July 13; published under the Creative Commons Attribution 3.0 Unported License. https://en.wikipedia.org/wiki/File:Blaise_Pascal_Versailles.JPG
This document is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.
The original LaTeX files and images used to create this reading are available at:
https://www.chrisspackman.com/educator-resources/readings/pascals-triangle/pascals-triangle-latex-files/